Introduction
This demo gives an overview of how to solve Sudoku puzzles using Cryptol’s interface to automated theorem provers.
Prerequisites
Before working through this lab, you’ll need
- Cryptol to be installed and
- this module to load successfully.
You’ll also need experience with
- loading modules and evaluating functions in the interpreter and
- the
:proveand:satcommands.
Skills You’ll Learn
By the end of this demo you’ll understand a bit more about how Cryptol can use its interface to automated theorem provers to perform computation. Rather than write a search algorithm in Cryptol, one only needs to write a solution checker in Cryptol (much easier) and then let the automated theorem prover carry out the search.
Load This Module
This lab is a
literate Cryptol
document — that is, it can be loaded directly into the Cryptol
interpreter. Load this module from within the Cryptol interpreter
running in the cryptol-course directory with:
Loading module Cryptol
Cryptol> :m labs::Demos::Cryptol::Sudoku
Loading module Cryptol
Loading module Cryptol
Loading module labs::Demos::Cryptol::Sudoku
We start by defining a new module for this lab and importing some accessory modules that we will use:
module labs::Demos::Cryptol::Sudoku where
You do not need to enter the above into the interpreter; the previous
:m ... command loaded this literate Cryptol file automatically.
In general, you should run Xcryptol-session commands in the
interpreter and leave cryptol code alone to be parsed by :m ....
Sudoku in Cryptol
On 18 Mar 2009, Galois, Inc. blogged about how to apply Cryptol to solve Sudoku puzzles. Cryptol has advanced greatly since that time, but it can still be straightforwardly applied toward Sudoku. Here, we port the original blog entry to a Markdown-Literate Cryptol file, updating the code for syntax and new features and interjecting occasionally. We hope to have done justice to the original.
On with the program…
Solving Sudoku Using Cryptol
WEDNESDAY, MARCH 18, 2009
DOMAIN SPECIFIC LANGUAGES, FORMAL METHODS
Galois, Inc.Cryptol is a language tailored for cryptographic algorithms. Sudoku is a popular puzzle the reader is no-doubt already familiar with. We will offer no deep reason why anyone should try to solve Sudoku in Cryptol; other than the very fact that it’d be a shame if we couldn’t! Needless to say, Cryptol has not been designed for encoding search algorithms. Nonetheless, some of the features of Cryptol and its associated toolset make it extremely suitable for expressing certain constraint satisfaction problems very concisely; and Sudoku very nicely falls into this category.
Representing the board
A Sudoku board can be represented in a variety of ways. We will pick the simplest: A sequence of 9 rows, each of which has 9 elements storing the digits. Each digit will require 4 bits; since they range from 1 to 9. So, a good Cryptol type for a board is:
[9][9][4]
INTERJECTION
Please excuse us for a second. Cryptol has introduced type aliases.
Where the original blog represented a Sudoku number as [4], we will
substitute an alias, and similarly for other common structures:
/** number in [1..9]; 0 reserved (e.g. for blank) */
type SudokuNum = [4]
/** row, column, or 3x3 square of `Num` */
type SudokuGroup = [9]SudokuNum
/** 9x9 grid of `SudokuNum` */
type SudokuBoard = [9]SudokuGroup
(Cryptol 2.6.0 introduced modular
integers,
so Z 10 would also be a good choice for SudokuNum, but we retain
[4] to minimize disruption to the original article.)
Sorry, you were saying…?
In Cryptol-speak, this type simply represents a sequence of precisely 9 elements, each of which is a sequence of 9 elements themselves, each of which are 4-bit words. (Technically, the type
[4]also represents a sequence of precisely 4 elements, each of which are bits. But it’s easier to read that as 4-bit words. The type[4]and[4]Bitare synonymous in Cryptol, and can be used interchangeably in all contexts.)Recognizing a valid row, column, or box
Let us tackle a much simpler problem to start with. How would we determine if a given set of 9 numbers form a valid Sudoku row, column, or a box? We should simply check that each number from 1 to 9 appears precisely once in the sequence:
check : SudokuGroup -> Bit
check group = [ contains x | x <- [1 .. 9] ] == ~zero
where contains x = [ x == y | y <- group ] != zero
We simply iterate over the numbers 1 through 9, and check that the given group contains that number. The function
containsiterates through all the elements in the given group, and makes sure one of them is the currently looked for element. (The Cryptol primitivezerois a polymorphic constant representing allFalses. The operator~inverts all the bits. Hence, the test== ~zeromakes sure all the components areTrue; and the test!= zeromakes sure at least one bit isTrue.)
INTERJECTION
Cryptol 2.6.0 also merged Cryptol::Extras into the Prelude (the
base module for Cryptol). Cryptol::Extras has numerous utility
functions, including these and more:
anyandall, which check a bit sequence to determine whether any or all of the elements respectively satisfy a given predicateelem, which returns whether an item is in a sequencemap, which applies a function to all items in a sequence, returning the sequence of values returned by the function
So currently, this function could also be defined in terms of simple, reusable helpers as:
/** whether finite sequence `G` contains element `x` */
contains' :
{a, n}
(Cmp a, fin n) =>
[n]a -> a -> Bit
contains' G x =
elem x G
/**
* whether finite sequence `G` contains all items in finite
* sequence `H`
*/
supset' :
{a, n}
(Cmp a, fin n) =>
[n]a -> [n]a -> Bit
supset' G H =
all (contains' G) H
/** whether `SudokuGroup` `G` contains one of each number 1-9 */
check' :
SudokuGroup -> Bit
check' G =
supset' G [1..9]
Using elem, contains' checks whether any item in G is equal to
x (satisfies (==) x). contains is a curried function, so
contains' G checks whether G contains the argument being passed,
and supset' maps this over H to determine if G contains all
items in H.
As a sanity check, we can confirm these are equivalent:
/** `check` and `check'` are equivalent. */
check_equiv : SudokuGroup -> Bit
property check_equiv = check === check'
For functions f and g of one argument, f === g is True iff
for all x, f x == g x.
Anyway, sorry for the interruption.
Recognizing a full board
Given a full Sudoku board, checking it’s a valid solution simply amounts to identifying rows, columns, and squares; and
check-ing them all, in the above sense. The following Cryptol function accomplishes this task rather concisely:
valid : SudokuBoard -> Bit
valid rows = [ check grp | grp <- rows # columns # squares ] == ~zero
where
columns = transpose rows
regions = transpose [ groupBy`{3} row | row <- rows ]
squares = [ join sq | sq <- groupBy`{3} (join regions) ]
The function
validreceives 9 rows; and calls check on all these rows, columns, and the squares. Columns are easy to compute: we simply use Cryptol’stransposeprimitive. The squares are slightly more tricky, but not particularly hard. We first group all the rows in length 3 segments, and transpose these to align them, thus forming the regions. Then the squares are simply grouping of the regions 3 elements at a time. It’s a good exercise to precisely work out how the squares are formed using the above code, something we encourage the interested reader to do on a rainy afternoon..
INTERJECTION
We can use all and map here to simplify valid:
valid' : SudokuBoard -> Bit
valid' rows = all check (rows # columns # squares)
where
columns = transpose rows
regions = transpose (map groupBy`{3} rows)
squares = map join (groupBy`{3} (join regions))
valid_equiv:
SudokuBoard -> Bit
property valid_equiv =
valid === valid'
Alright, enough out of us.
Solving Sudoku
All we have done so far is to recognize a given Sudoku board as valid; we have not written a single line of code to actually fill a partially empty board. The good news is that we do not need to! We have all the bits and pieces ready to go. Sounds too good to be true? Well, read on!
Enter Formal Methods
What if I told you that recognizing a valid Sudoku board is sufficient to actually solve one that has empty squares on it, using Cryptol’s formal-methods toolbox? The idea is rather simple. But before we get there, we need to take a detour into the Cryptol toolbox.
Checking satisfiability
Cryptol’s formal-methods tools can perform equivalence, safety, and satisfiability checking. We have talked about the former two in an earlier post. Today, we will look at satisfiability checking only. Given a function
f, the satisfiability checking problem asks if there is anyxsuch thatf x = True. Here is a simple example. Let:
f : [8] -> Bit
f x = x*x - 7*x + 12 == 0
The function
freturnsTrueif its given 8-bit argument is a solution to the quadratic equationx^^2 - 7x + 12 = 0. We have:
labs::Demos::Cryptol::Sudoku> :s base=10
labs::Demos::Cryptol::Sudoku> :sat f
Satisfiable
f 4 = True
(Total Elapsed Time: 0.151s, using "Z3")
Indeed, 4 is a solution to this equation. Is there any other solution? It is easy to formulate a similar query using the lambda notation:
labs::Demos::Cryptol::Sudoku> :sat (\x -> f x && (x != 4))
Satisfiable
(\x -> f x && (x != 4)) 3 = True
(Total Elapsed Time: 0.034s, using "Z3")
Cryptol tells us 3 is a solution as well! There happen to only be two solutions to this equation; let’s verify:
labs::Demos::Cryptol::Sudoku> :sat (\x -> f x && (x != 4) && (x != 3))
Unsatisfiable
(Total Elapsed Time: 0.034s, using "Z3")
Indeed, Cryptol confirms that 3 and 4 are the only 8-bit values that satisfy the equation
x^^2 - 7x + 12 = 0. (I should mention that the:satcommand is available only in thesymbolicandsbvbackends of Cryptol; the two main backends of Cryptol that are capable of performing formal-verification.)Back to Sudoku
Remember the valid function that returns
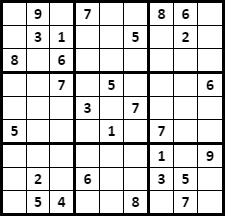
Trueif a given full board is a correctly laid-out Sudoku board? With the magic of satisfiability checking, we can just use that definition to fill in the blanks for us! To illustrate, consider the board below.
How do we encode a board with empty cells in Cryptol? One simple idea is to represent the board as a function: It will take the values of its “empty” cells, and return the full board. In the Cryptol encoding below I have tried to align the variables so that they correspond exactly to the empty cells, and named them row-by-row:
/** This puzzle from the Cryptol blog has a solution. */
puzzle :
[_]SudokuNum -> Bit
puzzle
[a1, a3, a5, a6, a9,
b1, b4, b5, b7, b9,
c2, c4, c5, c6, c7, c8, c9 ,
d1, d2, d4, d6, d7, d8 ,
e1, e2, e3, e5, e7, e8, e9,
f2, f3, f4, f6, f8, f9 ,
g1, g2, g3, g4, g5, g6, g8 ,
h1, h3, h5, h6, h9,
i1, i4, i5, i7, i9] =
valid
[[a1, 9, a3, 7, a5, a6, 8, 6, a9],
[b1, 3, 1, b4, b5, 5, b7, 2, b9],
[ 8, c2, 6, c4, c5, c6, c7, c8, c9],
[d1, d2, 7, d4, 5, d6, d7, d8, 6],
[e1, e2, e3, 3, e5, 7, e7, e8, e9],
[ 5, f2, f3, f4, 1, f6, 7, f8, f9],
[g1, g2, g3, g4, g5, g6, 1, g8, 9],
[h1, 2, h3, 6, h5, h6, 3, 5, h9],
[i1, 5, 4, i4, i5, 8, i7, 7, i9]]
INTERJECTION
Here, we introduce an _, which leaves it to Cryptol’s type verifier
to resolve a detail we don’t especially care about. There must be
some number of cells to fill in (in this case, 53), but that there
happen to be 53 in this case is irrelevant.
Ahem…sorry.
It might take a bit of staring at this definition; but the idea is strikingly simple. Notice that the type of puzzle is
[53][4] -> Bit, precisely because there are 53 empty cells. Also, instead of just returning the final board, I simply pass it to the functionvalid; so that the functionpuzzlewill returnTrueprecisely when it is given the correct numbers that solve it! By now, it must be obvious how we’ll solve Sudoku in Cryptol: All we need to do is to ask Cryptol to find the right input value to make the function returnTrue, i.e., we need to find a satisfying assignment. Here’s the response from Cryptol:
labs::Demos::Cryptol::Sudoku> :sat puzzle
Satisfiable
puzzle
[2, 5, 4, 3, 1, 4, 8, 6, 9, 7, 7, 1, 9, 2, 5, 4, 3, 3, 8, 4, 9, 2,
1, 6, 1, 2, 8, 4, 9, 5, 4, 9, 2, 6, 3, 8, 7, 6, 3, 5, 2, 4, 8, 9,
8, 7, 1, 4, 1, 9, 3, 6, 2] = True
(Total Elapsed Time: 0.910s, using "Z3")
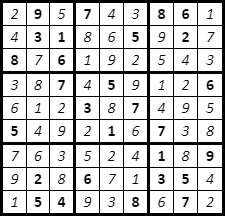
If we plug-in the numbers we get from Cryptol back into the grid, we get the full solution depicted below. (I used italic for the numbers found by Cryptol.) Well; that’s what we set out to do originally; so mission accomplished!
INTERJECTION
For kicks and giggles, let’s introduce a property saying the solution is unique:
/** a solution to the easy puzzle */
puzzle_solution :
SudokuBoard
puzzle_solution =
[[2, 9, 5, 7, 4, 3, 8, 6, 1],
[4, 3, 1, 8, 6, 5, 9, 2, 7],
[8, 7, 6, 1, 9, 2, 5, 4, 3],
[3, 8, 7, 4, 5, 9, 2, 1, 6],
[6, 1, 2, 3, 8, 7, 4, 9, 5],
[5, 4, 9, 2, 1, 6, 7, 3, 8],
[7, 6, 3, 5, 2, 4, 1, 8, 9],
[9, 2, 8, 6, 7, 1, 3, 5, 4],
[1, 5, 4, 9, 3, 8, 6, 7, 2]]
/** The easy puzzle's solution is valid. */
puzzle_solution_valid :
Bit
property puzzle_solution_valid =
valid puzzle_solution
/** The easy puzzle's solution is unique. */
puzzle_unique :
[_]SudokuNum -> Bit
property puzzle_unique
[a1, a3, a5, a6, a9,
b1, b4, b5, b7, b9,
c2, c4, c5, c6, c7, c8, c9 ,
d1, d2, d4, d6, d7, d8 ,
e1, e2, e3, e5, e7, e8, e9,
f2, f3, f4, f6, f8, f9 ,
g1, g2, g3, g4, g5, g6, g8 ,
h1, h3, h5, h6, h9,
i1, i4, i5, i7, i9] =
solution == puzzle_solution \/ ~ valid solution
where
solution =
[[a1, 9, a3, 7, a5, a6, 8, 6, a9],
[b1, 3, 1, b4, b5, 5, b7, 2, b9],
[ 8, c2, 6, c4, c5, c6, c7, c8, c9],
[d1, d2, 7, d4, 5, d6, d7, d8, 6],
[e1, e2, e3, 3, e5, 7, e7, e8, e9],
[ 5, f2, f3, f4, 1, f6, 7, f8, f9],
[g1, g2, g3, g4, g5, g6, 1, g8, 9],
[h1, 2, h3, 6, h5, h6, 3, 5, h9],
[i1, 5, 4, i4, i5, 8, i7, 7, i9]]
labs::Demos::Cryptol::Sudoku> :prove puzzle_unique
Q.E.D.
(Total Elapsed Time: 0.813s, using "Z3")
But let’s be honest: that puzzle is pretty easy. Let’s throw in a harder puzzle by Arto Inkala that garnered some publicity in 2010 as the “World’s Hardest Sudoku”. As recently as 2019, solving this with a dedicated program (albeit to be fair, on a phone app) in under two minutes evidently merits a YouTube video. Let’s see how Cryptol, a SAT solving interface that was not optimized for Sudoku puzzles in particular, fares…
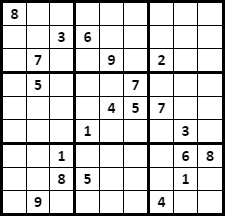
/**
* Arto Inkala's ["World's Hardest Sudoku"](
* https://www.conceptispuzzles.com/index.aspx?uri=info/article/424)
* has a solution.
*/
hard_puzzle :
[_]SudokuNum -> Bit
hard_puzzle
[ a2, a3, a4, a5, a6, a7, a8, a9,
b1, b2, b5, b6, b7, b8, b9,
c1, c3, c4, c6, c8, c9,
d1, d3, d4, d5, d7, d8, d9,
e1, e2, e3, e4, e8, e9,
f1, f2, f3, f5, f6, f7, f9,
g1, g2, g4, g5, g6, g7,
h1, h2, h5, h6, h7, h9,
i1, i3, i4, i5, i6, i8, i9] =
valid
[[ 8, a2, a3, a4, a5, a6, a7, a8, a9],
[b1, b2, 3, 6, b5, b6, b7, b8, b9],
[c1, 7, c3, c4, 9, c6, 2, c8, c9],
[d1, 5, d3, d4, d5, 7, d7, d8, d9],
[e1, e2, e3, e4, 4, 5, 7, e8, e9],
[f1, f2, f3, 1, f5, f6, f7, 3, f9],
[g1, g2, 1, g4, g5, g6, g7, 6, 8],
[h1, h2, 8, 5, h5, h6, h7, 1, h9],
[i1, 9, i3, i4, i5, i6, 4, i8, i9]]
labs::Demos::Cryptol::Sudoku> :s base=10
labs::Demos::Cryptol::Sudoku> :sat hard_puzzle
Satisfiable
hard_puzzle
[1, 2, 7, 5, 3, 6, 4, 9, 9, 4, 8, 2, 1, 7, 5, 6, 5, 4, 1, 8, 3, 1,
4, 2, 3, 8, 9, 6, 3, 6, 9, 8, 2, 1, 2, 8, 7, 6, 9, 5, 4, 5, 2, 9,
7, 4, 3, 4, 3, 2, 6, 9, 7, 7, 6, 3, 1, 8, 5, 2] = True
(Total Elapsed Time: 2.031s, using "Z3")
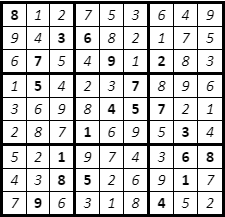
Not bad. Finally, we should prove that this is unique as well…
/** a solution to the "World's Hardest Sudoku" */
hard_solution :
SudokuBoard
hard_solution =
[[8, 1, 2, 7, 5, 3, 6, 4, 9],
[9, 4, 3, 6, 8, 2, 1, 7, 5],
[6, 7, 5, 4, 9, 1, 2, 8, 3],
[1, 5, 4, 2, 3, 7, 8, 9, 6],
[3, 6, 9, 8, 4, 5, 7, 2, 1],
[2, 8, 7, 1, 6, 9, 5, 3, 4],
[5, 2, 1, 9, 7, 4, 3, 6, 8],
[4, 3, 8, 5, 2, 6, 9, 1, 7],
[7, 9, 6, 3, 1, 8, 4, 5, 2]]
/** The hard puzzle's solution is valid. */
hard_solution_valid:
Bit
property hard_solution_valid =
valid hard_solution
/** The "World's Hardest Sudoku" has a unique solution. */
hard_unique :
[_]SudokuNum -> Bit
property hard_unique
[ a2, a3, a4, a5, a6, a7, a8, a9,
b1, b2, b5, b6, b7, b8, b9,
c1, c3, c4, c6, c8, c9,
d1, d3, d4, d5, d7, d8, d9,
e1, e2, e3, e4, e8, e9,
f1, f2, f3, f5, f6, f7, f9,
g1, g2, g4, g5, g6, g7,
h1, h2, h5, h6, h7, h9,
i1, i3, i4, i5, i6, i8, i9] =
solution == hard_solution \/ ~ valid solution
where
solution =
[[ 8, a2, a3, a4, a5, a6, a7, a8, a9],
[b1, b2, 3, 6, b5, b6, b7, b8, b9],
[c1, 7, c3, c4, 9, c6, 2, c8, c9],
[d1, 5, d3, d4, d5, 7, d7, d8, d9],
[e1, e2, e3, e4, 4, 5, 7, e8, e9],
[f1, f2, f3, 1, f5, f6, f7, 3, f9],
[g1, g2, 1, g4, g5, g6, g7, 6, 8],
[h1, h2, 8, 5, h5, h6, h7, 1, h9],
[i1, 9, i3, i4, i5, i6, 4, i8, i9]]
labs::Demos::Cryptol::Sudoku> :prove hard_unique
Q.E.D.
(Total Elapsed Time: 5.431s, using "Z3")
Okay then. Let’s defer to the original for some closing remarks…
What just happened here?
Apologies if you were expecting to see Cryptol code that actually searched for the values of the empty cells! Note that we have not written a single line of code that tried to deduce what must go in the empty cells, nor have we implemented a search algorithm. We merely viewed Sudoku as a satisfiability problem, and asked Cryptol’s formal-methods tools to find the missing values for us. The necessary search is all done by the underlying formal-methods engine, freeing us from the labor. Yet another instance of telling the computer “what” to do, instead of “how.”
[
Downloadsection with broken link removed]
Solicitation
How was your experience with this lab? Suggestions are welcome in the form of a ticket on the course GitHub page: https://github.com/weaversa/cryptol-course/issues
From here, you can go somewhere!
| ^ Cryptol Demos | ||
| < n-Queens | Sudoku |